Category Theory and Human Behavior

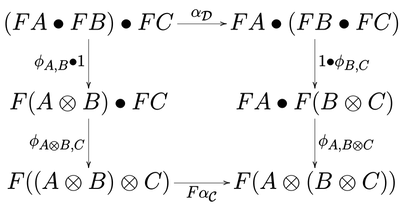
Just Keep Reading, It’s Really Not That Complicated

Here’s one way category theory applies to human behavior. I’m going to genericize this and apply an example using javascript – don’t fret, it will be very simple. You should be able to understand this without programming. Now let’s say that you need to acquire 3 pieces of information – Alpha, Beta, and Gamma. It doesn’t really matter what pieces of information Alpha, Beta, and Gamma – it could be anything. This is a generic example.

Let’s write this out with javascript:

function myBehavior() {
  me.askFor('Alpha');
  me.askFor('Beta');
  me.askFor('Gamma');
}

And let’s say that you’re afraid that asking for this information will alert this person to your intentions. Now, let’s say you have some people you have influence over – your unwitting minions Alice, Bob and Carol – mwua haha ha. Well, then, let’s apply the Category Theory concept of Functors to abstract this behavior and obfuscate it.

function myNewBehavior() {
  me.ask('Alice').toAskFor('Alpha');
  me.ask('Bob').toAskFor('Beta');
  me.ask('Carol').toAskFor('Gamma');
}

Congratulations, you’ve just basically used your minions to abstract your behavior and hide your motivations. If the person you’re acquiring information from knew you wanted to know about Alpha, Beta and Gamma, then they could also conclude you were going to Zeta sometime soon. I apologize – things get confusing when you’re dealing with abstract nonsense.

Interestingly, these same concepts also apply to computer hacking, where you need to outwit automated algorithms for detecting abnormal behavior – and you do so using Agent-based Design Patterns …

… ** aaaand a botnet. ** You’re going to need a botnet.

Functors and Natural Transformations

So, in the code sample above, we’ve just applied the Agent-based Design Pattern to our original function myBehavior as a *Category Theory *Functor **. And now we have a new function called myNewBehavior.

At least, I think Functor is the right term, but I might actually be referring to Natural Transformations – I DON’T EVEN KNOW LMAO. The details of how Functors work aren’t really important – but they are incredibly useful, if you understand them.

This is getting complicated, but if you’re into computer science, you can use Abstract Syntax Trees (AST’s) to basically modify any existing code written in any programming language and add functionality to it. You could theoretically wrap any function with code for Dynamic Programming. You could even transform it to another programming language. It’s !@#$’ing magic. It is, however, overly complicated and 999 times out of 1,000, there is an easier way to do things. It ain’t easy, that’s for sure. I’ve never done it.

<gives audience generous pause for laughter>

My point is that category theory underpins human behavior – conversation, interaction, motivation, sociology, etc. All of these can be mathematically described using tree-like structures representing self-modifying functions, coupled with game theory and other mathematic concepts. Category theory is also applicable in genericizing and amalgamating other behavior that you see. You can basically interpret any behavior as a function, then replace the specifics with variables and combine with other functions to reuse it.

If you don’t understand this math – that’s OK. That’s what’s nice about having a human brain – you don’t actually have to understand how its functionality works to use it. You just do. By the time you pop out and before you start crawling, your brain is already capable of linear algebra, category theory and other complex concepts, many of which are still far beyond human understanding. If your brain wasn’t capable of these things, you wouldn’t be able to learn to walk or cross the street.

Make It Stop!! LOL I’m kidding, I’m kidding.

This is what I’ve been seeing in my head for the past few months. Well, this and several kinds of more complicated, high dimensional graph structures.

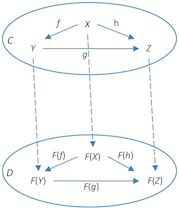
Functors are mappings between multiple categories. Between any two “finite” categories – that is, two categories with a finite set of objects and a finite number of mappings (morphisms) between those objects – there is a finite number of functors encompassing the set of all functors between them. These represent the myriad of ways to combinate between one category to the next … mayyybe. Jeez, I should maybe learn a little more about this so I $#@!’ing know what I’m talking about. I should – idonno – go to college or something. Or at least be surrounded by other people who do know what the !@#$ they’re talking about!

Oh, Irony

See – the ironic part is that I’ve never really been able to intuitively understand social behavior. Yet, now that I’ve been able to intellectualize it, I can become more profient than most ordinary people who aren’t able to intellectualize it.

And now, for your daily dose of “Google, I’m Feeling Lucky”

Kagamine Rin - Abstract Nonsense (English Subbed)

Yeesh …. On second thought, there’s some really bad imagery in that video. Dammit. Read the lyrics, pay no attention to the pictures in the video. There really are some relevant subjects intermingled between the bullshit. Gee, thanks Google.

Up next, abusing the equals function to actually make category theory useful.

Equals is a function too, donchya kno?!